Tritos
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (October 2024) |

The tritos is an eclipse cycle of 3,986.628 days (about 10 years, 11 months). It corresponds to:
- 135 synodic months
- 146.50144 draconic months
- 11.50144 eclipse years (23 eclipse seasons)
- 144.68135 anomalistic months.
The length of the tritos is equal to the length of the inex minus the length of the saros eclipse cycles. Therefore, eclipses that occur 1 tritos apart (i.e. both eclipses belong to the same tritos series), belong to two different saros series with series numbers that differ by one.
The pre-Columbian Maya used a calculation in their own observations of eclipse cycles in which a period of three tritoses (or tritoi) was approximated by 11960 days, based on 46 periods of their tzolk'in calendar (i.e. 46 × 260 days). The number of anomalistic months in a tritos (144.68), having a fraction near 2⁄3, means every third eclipse is in nearly the same position in the elliptical orbit, so eclipses will have similar timing and total versus annular quality.
Solar and lunar eclipse event dates will repeat on this cycle for about 700 years.
Example solar Tritos series
[edit]This eclipse is a part of a tritos cycle, repeating at alternating nodes every 135 synodic months (≈ 3986.63 days, or 11 years minus 1 month). Their appearance and longitude are irregular due to a lack of synchronization with the anomalistic month (period of perigee), but groupings of 3 tritos cycles (≈ 33 years minus 3 months) come close (≈ 434.044 anomalistic months), so eclipses are similar in these groupings.
| Series members between 1801 and 2200 | ||||
|---|---|---|---|---|
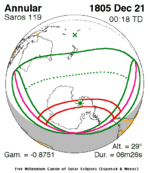 December 21, 1805 (Saros 119) |
 November 19, 1816 (Saros 120) |
 October 20, 1827 (Saros 121) |
 September 18, 1838 (Saros 122) |
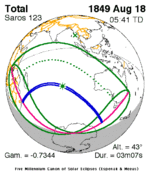 August 18, 1849 (Saros 123) |
 July 18, 1860 (Saros 124) |
 June 18, 1871 (Saros 125) |
 May 17, 1882 (Saros 126) |
 April 16, 1893 (Saros 127) |
 March 17, 1904 (Saros 128) |
 February 14, 1915 (Saros 129) |
 January 14, 1926 (Saros 130) |
 December 13, 1936 (Saros 131) |
 November 12, 1947 (Saros 132) |
 October 12, 1958 (Saros 133) |
 September 11, 1969 (Saros 134) |
 August 10, 1980 (Saros 135) |
 July 11, 1991 (Saros 136) |
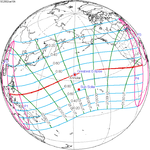 June 10, 2002 (Saros 137) |
 May 10, 2013 (Saros 138) |
 April 8, 2024 (Saros 139) |
 March 9, 2035 (Saros 140) |
 February 5, 2046 (Saros 141) |
 January 5, 2057 (Saros 142) |
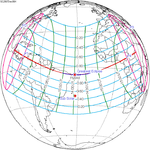 December 6, 2067 (Saros 143) |
 November 4, 2078 (Saros 144) |
 October 4, 2089 (Saros 145) |
 September 4, 2100 (Saros 146) |
 August 4, 2111 (Saros 147) |
 July 4, 2122 (Saros 148) |
 June 3, 2133 (Saros 149) |
 May 3, 2144 (Saros 150) |
 April 2, 2155 (Saros 151) |
 March 2, 2166 (Saros 152) |
 January 29, 2177 (Saros 153) |
 December 29, 2187 (Saros 154) |
 November 28, 2198 (Saros 155) | |||
Example lunar Tritos series
[edit]This eclipse is a part of a tritos cycle, repeating at alternating nodes every 135 synodic months (≈ 3986.63 days, or 11 years minus 1 month). Their appearance and longitude are irregular due to a lack of synchronization with the anomalistic month (period of perigee), but groupings of 3 tritos cycles (≈ 33 years minus 3 months) come close (≈ 434.044 anomalistic months), so eclipses are similar in these groupings.
| Series members between 1801 and 2200 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1804 Jan 26 (Saros 111) |
1814 Dec 26 (Saros 112) |
1825 Nov 25 (Saros 113) |
1836 Oct 24 (Saros 114) |
1847 Sep 24 (Saros 115) | |||||
| 1858 Aug 24 (Saros 116) |
1869 Jul 23 (Saros 117) |
1880 Jun 22 (Saros 118) |
1891 May 23 (Saros 119) |
1902 Apr 22 (Saros 120) | |||||

|

| ||||||||
| 1913 Mar 22 (Saros 121) |
1924 Feb 20 (Saros 122) |
1935 Jan 19 (Saros 123) |
1945 Dec 19 (Saros 124) |
1956 Nov 18 (Saros 125) | |||||

|

|

|

|

|

|

|

|

|

|
| 1967 Oct 18 (Saros 126) |
1978 Sep 16 (Saros 127) |
1989 Aug 17 (Saros 128) |
2000 Jul 16 (Saros 129) |
2011 Jun 15 (Saros 130) | |||||

|

|

|

|

|

|

|

|

|

|
| 2022 May 16 (Saros 131) |
2033 Apr 14 (Saros 132) |
2044 Mar 13 (Saros 133) |
2055 Feb 11 (Saros 134) |
2066 Jan 11 (Saros 135) | |||||

|

|

|

|

|

|

|

|

|

|
| 2076 Dec 10 (Saros 136) |
2087 Nov 10 (Saros 137) |
2098 Oct 10 (Saros 138) |
2109 Sep 09 (Saros 139) |
2120 Aug 09 (Saros 140) | |||||

|

|

|

|

|

|
||||
| 2131 Jul 10 (Saros 141) |
2142 Jun 08 (Saros 142) |
2153 May 08 (Saros 143) |
2164 Apr 07 (Saros 144) |
2175 Mar 07 (Saros 145) | |||||
| 2186 Feb 04 (Saros 146) |
2197 Jan 04 (Saros 147) | ||||||||
See also
[edit]- Eclipse cycle
- Inex - related series
References
[edit]- Mathematical Astronomy Morsels, Jean Meeus, Willmann-Bell, Inc., 1997 (Chapter 9, p. 51, Table 9.A Some eclipse Periodicities)
